r.v.s.: random variable sequence

i.i.d: individual identical distribution

w.p.: with probability

PMF (Probability Mass Function) $P(X=x)$

CDF (Cumulative Distribution Function) $P(X \leq x)$

PDF (Probability Density Function) derivate of CDF

PGF (Probability Generating Function) $E(t^X) = \sum_{k=0}^{\infty} p_k t^k$

MGF (Moment Generating Function) $M(t) = E(e^{tX})$

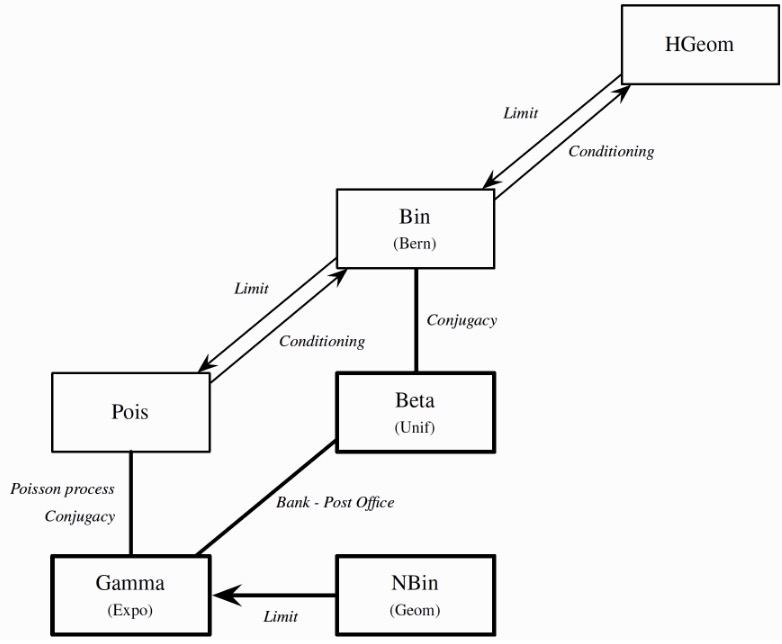
Distributions

• Binomial Distribution $X\sim B(n,p)$: number of success in n trails
• HyperGeometric Distribution $X\sim HGeom(w,b,n)$: draw n balls between w white and b black
• Geometric Distribution $X\sim Geom(p)$: number of the Bernoulli trails before success (First Success Distribution)
• Negative Binomial Distribution $X\sim NBin(r,p)$: number of the Bernoulli trails before $r^{th}$ success
• Poisson Distribution $X\sim Pois(\lambda)$: number of times an event occurs in an interval of time or space
• Uniform Distribution $U\sim Unif(a,b)$: Distribution on the interval $(a,b)$
• Standard Normal Distribution $X\sim N(0,1)$
• Normal Distribution $X\sim N(\mu,\sigma^2)$
• Beta Distribution $X\sim Beta(a,b)$
• Multinomial Distribution $\mathbf{X}\sim Mult_k(n,\mathbf{p})$