---

Defination of Conditonal Probability

Defination Two events $A$ and $B$, with $P(B)>0$, the conditional probability of $A$ given $B$ , denoted by $P(A|B)$, is defined as :

$$P(A|B)=\frac{P(AB)}{P(B)}$$

• $P(A)$: prior probability
• $P(A|B)$: posterior probability

---

Bayes’ Rule & LOTP

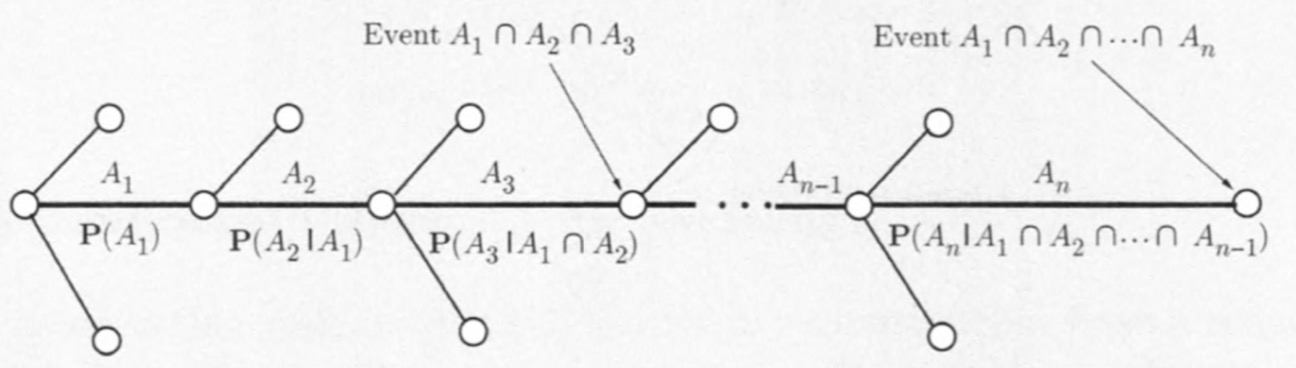
Chain Rule

chain rule

$$P(A_1,...,A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1A_2)...P(A_n|A_1,...,A_{n-1})$$

Bayes’ Rule

$$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$$

LOTP (Law of Total Probability)

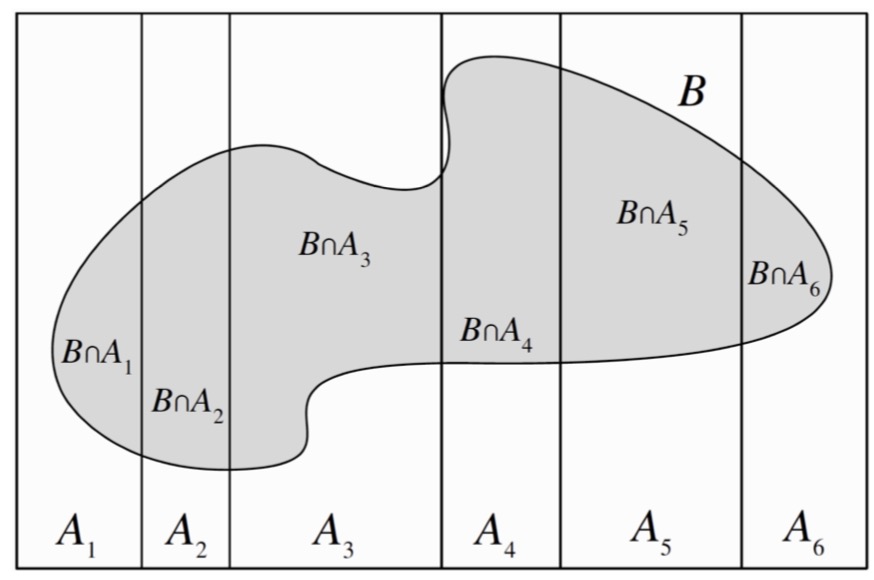
Theorem: Let $A_1,A_2,…,A_n$ be the partition of the sample space $S$, with $P(A_1)>0$, Then :

$$P(B) = \sum_i^n P(B|A_i)P(A_i)$$

Theorem: Let $A_1,A_2,…,A_n$ be the partition of the sample space $S$, for any event $B$ such that $P(B) > 0$, we have :

$$P(A_i|B) = \frac{P(A_i)P(B|A_i)}{P(A_1)P(B|A_1)+\dotsb+P(A_n)P(B|A_n)}$$

---

Conditional Probabilitiy

Conditional Probability is also the probability, so it inherent the property of probability (suppose the sample space is $S$):

• $P(S|E) = 1$ and $P(\emptyset|E) = 0$
• if events $A_1,…$ are disjoint, then $P(\cup_{j=1}^{\infty}A_j|E) = \sum_{j=1}^{\infty}P(A_j|E)$
• $P(A^c|E) = 1 - P(A|E)$
• Inclusion-Exclusion : $P(A\cup B|E) = P(A|E) + P(B|E) - P(A\cap B|E)$

Bayes’ Rule with Extra Condition:

Theorem: Provided that $P(A\cap E)>0$ and $P(B\cap E)>0$, we have:

$$P(A|B,E) = \frac{P(B|A,E)P(A|E)}{P(B|E)}$$

LOTP with Extra Condition:

Theorem: Let $A_1,A_2,…,A_n$ be the partition of the sample space $S$, with $P(A_i \cap E) >0$, Then:

$$P(B|E) = \sum_{i=1}^n P(B|A_i,E)P(A_i|E)$$

Approaches for $P(A|B,C)$

• $$P(A|B,C) = \frac{P(A,B,C)}{P(B,C)}$$
• $$P(A|B,C) = \frac{P(B|A,C)P(A|C)}{P(B|C)}$$
• $$P(A|B,C) = \frac{P(C|A,B)P(A|B)}{P(A|C)}$$

---

Independence of Events

Independence of Two Events

Defination: Events $A$ and $B$ are independent if

$$P(A\cap B) = P(A) P(B) \Leftrightarrow P(A|B) = P(A) , P(B|A) = P(B)$$

Independence vs Disjointness

• $A,B$ is disjoint : $P(A\cap B) = 0$
• $A,B$ is independent : $P(A) = 0, P(B) = 0$

Conditional Independence

Defination: Events $A$ and $B$ are conditionally independent given E if:

$$P(A\cap B|E) = P(A|E)P(B|E)$$ $$Contitional\ Independence \nRightarrow Independence$$ $$Independence \nRightarrow Contitional\ Independence$$