Nerual Style

There are two aspect for a image, one is the content of the image, which can be descriped as elements or object in the image, another is the style of the image, it might be abstract, and usually revealed by the painting skill or technique.

Shortly, we have two image, one for style while the other for content. now, we want to combine the style in image1 and the content in image2 together, and it can be achieved from deep neural net work, and we call it Neural Style.

Moreover we simply define the loss function care both style and content

$$L_{total} = \alpha L_{content}+\beta L_{style}$$

Now let’s have a look about what neural network can do here, and analysis the affect of $L_{content}$ and $L_{style}$ independently.

Suppose we have the content image, and send it to the neural network, it will have the responses in each layer by filters, we also construct a white noisy image, filter it in the same way, and define a loss $L_{content}$ between filtered content and filtered noisy, we take the noisy image as input,and it can update iterativly.

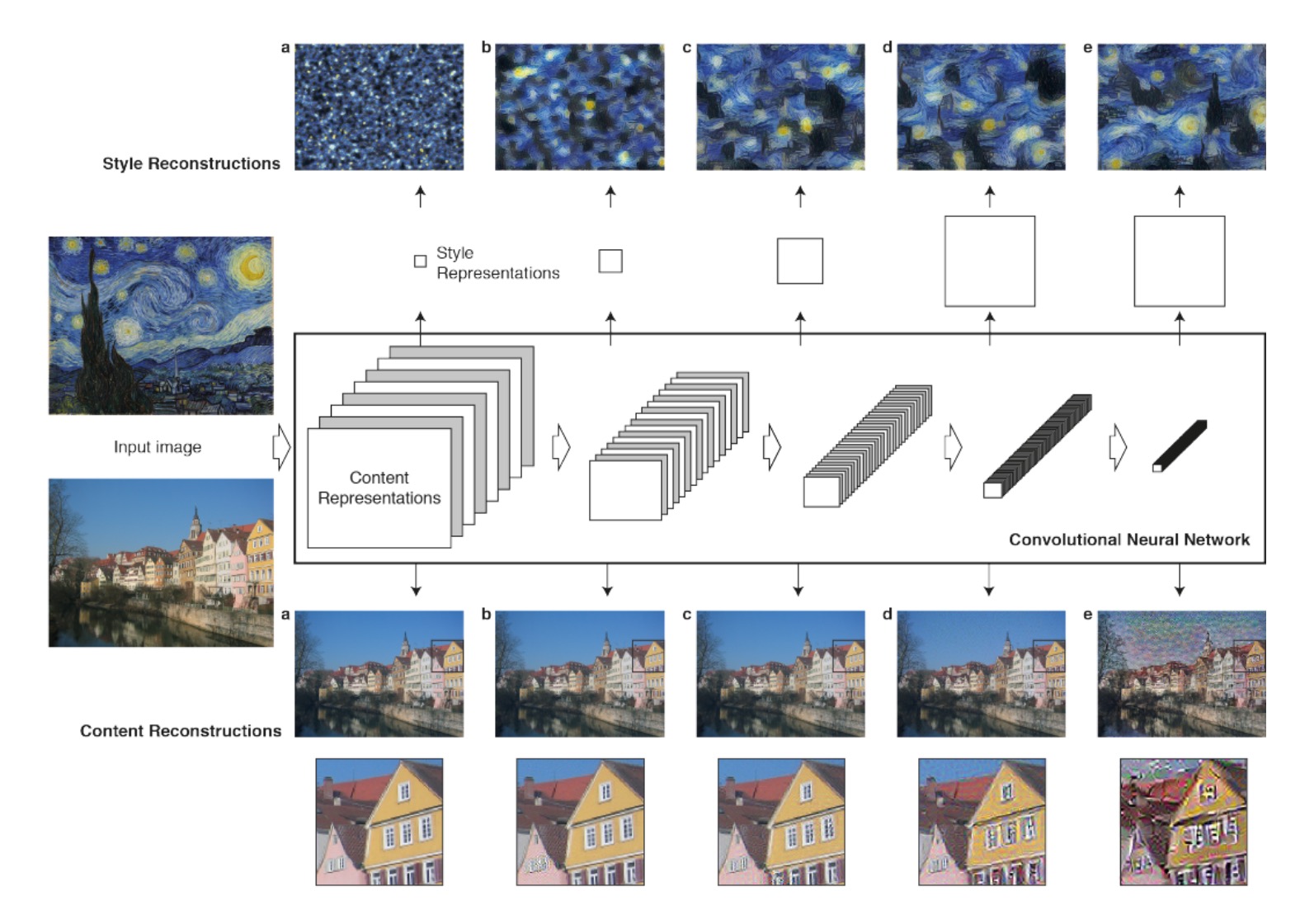
The image above show the reconstruction result between different layers, and reconstruction from lower layers(a,b,c) is alomost perfect, the style reconstruction may be more realistic in the deeper layer.

Let’s get familiar with some notion of the formulation first( suppse we are in the $l^{th}$ level of the net ):

• $\vec{p}$: Original content image (input)
  • $P^l$: Content feature representation in layer $l$ respect to $\vec{p}$
• $\vec{a}$: Original style image (input)
  • $A^l$: Style feature representation in layer $l$ respect to $\vec{a}$

• $\vec{x}$: Target image (output)

  • $F^l$: Content feature representation in layer $l$ respect to $\vec{x}$
  • $G^l$: Style feature representation in layer $l$ respect to $\vec{x}$
  • $F_{ij}^l$: Element of $i^{th}$ filter at $j^{th}$ position in layer $l$

• $N_l$: The number of the filters in the $l^{th}$ level

• $M_l$: The size of a feature map produced by a filter,usually it equals to $height \times weight$

The squared-error loss between two content feature representations is:

$$L_{content}(\vec{p},\vec{x},l) = \frac{1}{2} \sum_{i,j}(F_{ij}^l - P_{ij}^l)^2$$

In each layer, build a style representation compute the correlations between the different filter responses, which is called Gram Matrix $G^l\in R^{N_l \times N_l}$, and $G_{ij}^l$ is the inner product between the vectorized feature map between $i$ and $j$ in layer $l$

$$G_{ij}^l = \sum_k F_{ik}^l F_{jk}^l$$

Also we have

$$A_{ij}^l = \sum_k P_{ik}^l P_{jk}^l$$

The contribution of the layer to the total loss is

$$E_l = \frac{1}{4N_l^2 M_l^2 }\sum_{i,j}(G_{ij}^l - A_{ij}^l)^2$$

And the total loss is

$$L_{style}(\vec{a},\vec{x}) = \sum_{l=0}^L w_lE_l$$

Let’s focus more on the detail about the gradient of the loss:

The derivative of content loss respect to activations in layer l equals

$$\frac{\partial L_{content}}{\partial F_{ij}^l} = \left \{ \begin{array}{ll} (F^l - P^l)_{ij} & if\ F_{ij}^l > 0 \\ 0 & if\ F_{ij}^l < 0 \end{array} \right .$$

The derivative of style loss respect to activations in layer l equals

$$\frac{\partial E_l}{\partial F_{ij}^l} = \left \{ \begin{array}{ll} \frac{1}{N_l^2M_l^2}((F^l)^T(G^l - A^l))_{ij}& if\ F_{ij}^l > 0 \\ 0 & if\ F_{ij}^l < 0 \end{array} \right .$$

The final loss function we want to minimize is

$$L_{total}(\vec{p},\vec{a},\vec{x}) = \alpha L_{content}(\vec{p},\vec{x}) + \beta L_{style}(\vec{a},\vec{x})$$

---

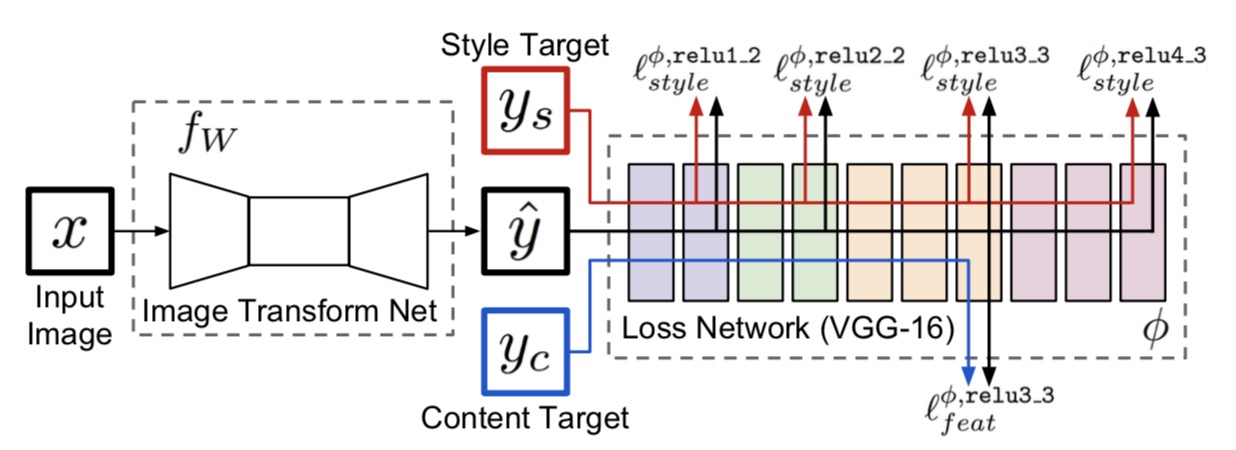
Fast Neural Style

FastNet