Bayesian Inference

Bayesian Inference Framework

We aim to extract information about $\Theta$, based on observing a collection $X = (X_1,…,X_n)$

• Unknow $\Theta$
  • treated as a random variable
  • prior distribution $p_\Theta$ or $f_\Theta$
• Observation $X$
  • observation model $p_X|\Theta$ or $f_X|\Theta$
• Use appropriate version of the bayes rule to find $p_{\Theta|X}(\cdot|X=x)$

Principal Bayesian Estimation Method

• Maximum a posterior probability (MAP) rule Select the possible parameter with maximum conditional/posterior probability given the data
• Least mean squares (LMS) estimation Select an estimator/function of the data that minimizes the mean squared error between the parameterand its estimate
  • $p_{\Theta|X}(\theta^*|x)=\mathop{max}_{\theta}p_{\Theta|X}(\theta|x)$

Example (Inferring the Unknown Bias of A Coin)

We wish to estimate the probability of heads, denoted by $p$, suppose the prior is a beta density with $a,b$, that is , $p \sim Beta(a,b)$. We consider n independent tosses and let $X$ be the number of heads observed

MAP Estimate The posterior PDF of $p$ has the form

$$\begin{align} f(p|X=k) &= \frac{P(X=k|p)f(p)}{P(X=k)}=\frac{\left( \begin{array}{c} n\\k \end{array} \right) p^k(1-p)^{n-k}\frac{1}{\beta(a,b)}p^{a-1}(1-p)^{b-1}}{P(X=k)} \\ &= c\cdot p^{a+k-1} (1-p)^{b+(n-k)-1} \end{align}$$

Hence the posterior density is beta with parameters $a+k$ and $b+(n-k)$

By MAP rule, we select the eatimator as

$$\hat{p}_{MAP} = \mathop{arg}\mathop{max}_p f(p|X=k) = \mathop{arg}\mathop{max}_p p^{a+k-1}(1-p)^{b+(n-k)-1}$$

Let $g(p) = p^{a+k-1}(1-p)^{b+(n-k)-1}$,then we have

$$log(g(p)) = (a+k-1)\mathop{log}p + (b+(n-k)-1)\mathop{log}(1-p)$$

To find $p^*$ let

$$\partial \frac{ \mathop{log}(g(p))} {\partial p}|_{p=p^*} = 0$$

which yields

$$\hat{p}_{MAP} = \frac{a+k-1}{a+b+n-2}$$

When the prior distribution of $p$ is $Unif(0,1)$, that is $a=0,b=0$, the estimator under MAP rule is $\hat{p}_{MAP} = \frac{k}{n}$

LMS Estimate By Beta-Binomial conjugacy, $f(p|X=k) \sim Beta(a+k,b+n-k)$, the expectation of random variable $Y\sim Beta(a,b)$ is $E(Y) = \frac{a}{a+b}$, we have

$$\hat{p}_{LMS} = E(p|X=k) = \frac{a+k}{(a+k)+(b+n-k)} = \frac{a+k}{a+b+k}$$

When the prior distribution of $p$ id $Unif(0,1)$, that is $a = 1,b = 1$, the estimator under MAP rule is $\hat{p}_{MAP} = \frac{k+1}{n+2}$

---

Classical Inference

• Classical Statistics: unknown constant $\theta$
  • also for vectors $X$ and $\theta$ : $p_{X_1,…,X_n}(x_1,…,x_n; \theta_1,…,\theta_m)$
  • $p_X(x;\theta)$ are NOT conditional probabilities; $\theta$ is not random
  • mathematically: many models, one for each possible value of $\theta$

For example, the data observation model is $X\sim Binomial(n,\theta)$, Then under each possible value of $\theta$, the candidate model is

$$p_X(x;\theta) = P(X=x;\theta) = \left( \begin{array}{c} n\\k \end{array} \right) \theta^x (1-\theta)^{n-x}$$

Classical Inference use the maximum likelihood to estimate the $\theta$

---

Sampling Moments

Definition (Moments)

Let $X$ be an r.v. with mean $\mu$ and variance $\sigma^2$, The $n^{th}$ moment of $X$ is $E(X^n)$, the $n^{th}$ central moment is $E((X-\mu)^n)$, and the $n^{th}$ standardized moment is $E((\frac{X-\mu}{\sigma})^n)$

Definition (Sample Moments)

Let $X_1,…,X_n$ be i.i.d. random variables, the $k^{th}$ sample moment is the

$$M_k = \frac{1}{n} \sum_{j=1}^n (X_j)^k$$

The sample mean $\bar{X}_n$ is the first sample moment:

$$\bar{X}_n = \frac{1}{n} \sum_{j=1}^n X_j$$

Theorem (Mean and Var of Sample Mean)

Let $X_1,…,X_n$ be i.i.d. r.v.s with unknown mean $\mu$ and variance $\sigma^2$. Then the sample mean $\bar{X}_n$ is unbiased for estimating $\mu$. That is

$$E(\bar{X}_n) = \mu$$

The variance is

$$Var(\bar{X}_n) = \frac{\sigma^2}{n}$$

Definition (Sample Variance)

Let $X_1,…,X_n$ be i.i.d. random variables. The sample variance is the r.v.

$$S_n^2 = \frac{1}{n-1} \sum_{j=1}^n (X_j-\bar{X}_n)^2$$

Theorem (Unbiaseness of Sample Var)

Let $X_1,…,X_n$ be i.i.d. r.v.s with unknown mean $\mu$ and variance $\sigma^2$. The Sample Var $S_n^2$ is unbiased for estimating $\sigma^2$

$$E(S_n^2) = \sigma^2$$

Definition (Convergence with Probability)

Let $X_1,X_2,…$ be random variables. $X_n$ converges almost surely (a.s.) to the random variable $X$ as $n\rightarrow \infty$ and only if

$$P(\left\{ \omega : X_n(\omega) \rightarrow X(\omega)\ as\ n\rightarrow \infty \right\}) = 1$$

Notation: $X_n \xrightarrow{a.s.} X \text{ as } n\rightarrow \infty$

Example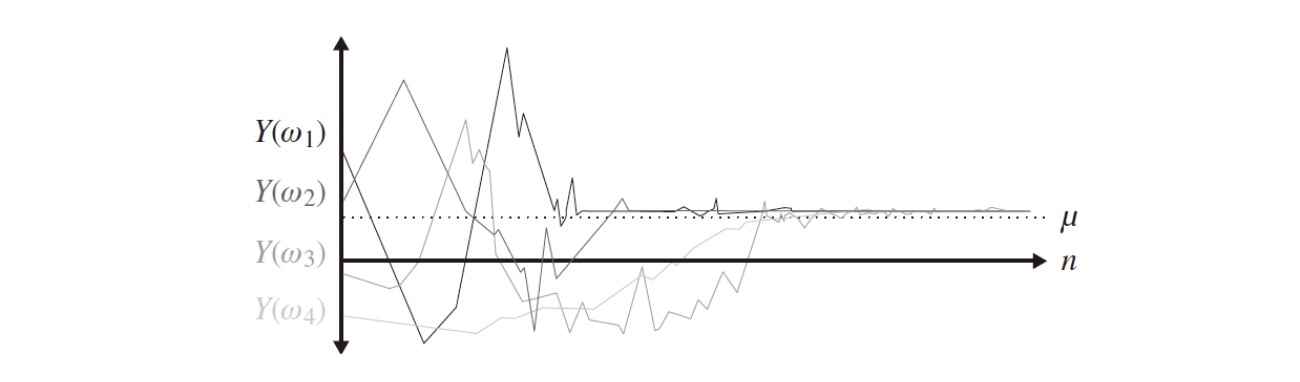

Definition (Convergence in Probability)

Let $X_1,X_2,…$ be random variables. $X_n$ converges in probability to the random variable $X$ as $n\rightarrow \infty$ if and only if for every $\epsilon >0$

$$P(|X_n-X|>\epsilon) \rightarrow0 \ as \ n\rightarrow \infty$$

Notation: $X_n \xrightarrow{P} X \text{ as } n\rightarrow \infty$

Example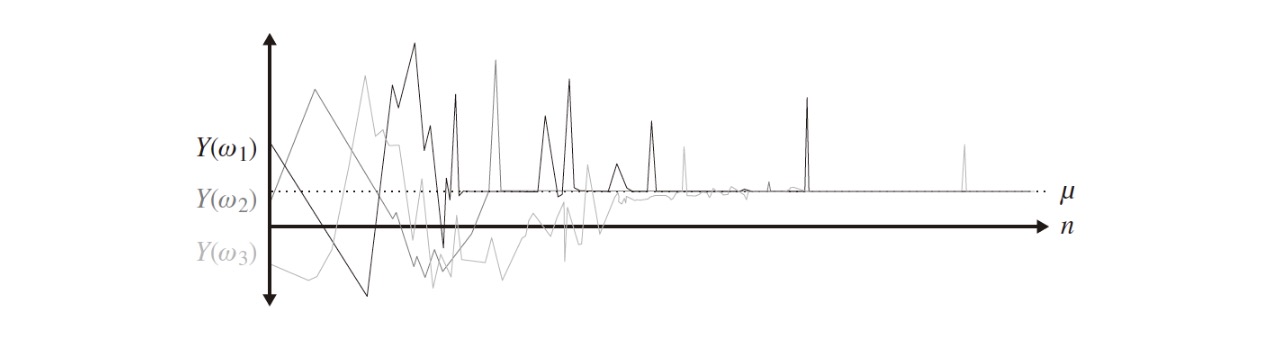

---

Law of large Numbers

Definition

Let $X_1,…,X_n$ be i.i.d. r.v. with finite mean $\mu$ and finite variance $\sigma^2$. The samplw mean $\bar{X}_n$ is defined as

$$\bar{X}_n = \frac{1}{n}\sum_{j=1}^n X_j$$

The Sample mean $\bar{X}_n$ is itself an r.v. with mean $\mu$ and variance $\sigma^2/n$

Theorem (Strong Law of Large Numbers)

The event $\bar{X}_n \rightarrow \mu$ has probability $1$

Theorem (Weak Law of Large Numbers)

For all $\epsilon >0, P(|\bar{X}_n - \mu>\epsilon) \rightarrow 0$ as $n\rightarrow \infty$

Definition (Time Average)

$$\bar{N}^{Time\ Average}(\omega)=\mathop{lim}_{t\rightarrow \infty} \frac{\int_0^t N(v,\omega)dv}{t}$$

Definition (Ensemble Average)

$$\bar{N}^{Ensemble}(\omega)=\mathop{lim}_{t\rightarrow\infty} E[N(t)]=\sum_{i=0}^{\infty} i p_i$$

---

Central Limit Theorem

Theorem (Central Limit)

As $n\rightarrow \infty$

$$\sqrt{n}\left( \frac{\bar{X}_n - \mu}{\sigma} \right) \rightarrow N(0,1)$$

CLT Approximation For a large $n$, the distribution od $\bar{X}_n$ is approximately $N(\mu,\sigma^2/n)$

Example (CLT Example)

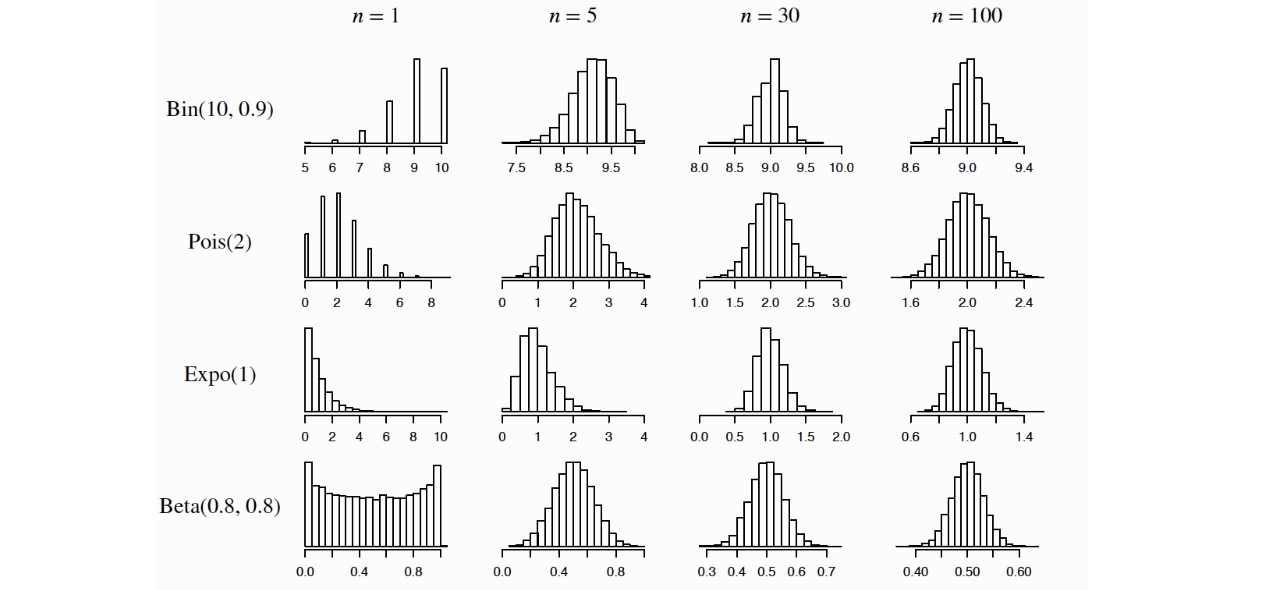
• Poisson Convergence to Normal Let $Y\sim Pois(n)$. Consider $Y$ as sum of $n$ i.i.d. $Pois(1)$ r.v.s. For large $n$: $$Y\sim N(n,n)$$
• Gamma Convergence to Normal Let $Y\sim Gamma(n,\lambda)$. Consider $Y$ as sum of $n$ i.i.d. $Expo(\lambda)$ r.v.s. For large $n$: $$Y\sim N(\frac{n}{\lambda},\frac{n}{\lambda^2})$$
• Binomial Convergence to Normal Let $Y\sim Bin(n,p)$. Consider $Y$ as sum of $n$ i.i.d. $Bern(p)$ r.v.s. For large $n$: $$Y\sim N(np,np(1-p))$$

De Moivre-Laplace Approximation

$$\begin{align} P(Y=k) &= P(k-\frac{1}{2} < Y < k + \frac{1}{2}) \\ &\approx \Phi\left( \frac{k+\frac{1}{2} - np}{\sqrt{np(1-p)}} \right) -\Phi\left( \frac{k-\frac{1}{2} - np}{\sqrt{np(1-p)}} \right) \end{align}$$

• Possion Approximation When $n$ is large and $p$ is samll
• Normal Approximation When $n$ is large and $p$ is around $1/2$

---

Inequality

Basic Inequalities

• Cauchy-Schwarz Inequality

  $$|E(XY)| \leq \sqrt{E(X^2)E(Y^2)}$$

• Jensen’s Inequality

  • If $g$ is a convex function and $X$ is a r.v. then $$E(g(x)) \geq g(E(X))$$
  • If $g$ is a concave function $$E(g(x)) \leq g(E(X))$$

• Markov’s Inequality

  $$P(|X|\geq a) \leq \frac{E|X|}{a}$$

• Chebyshev’s Inequality Let $X$ have mean $\mu$ and variance $\sigma^2$

  $$P(|X-\mu|\geq a) \leq \frac{\sigma^2}{a^2}$$

• Chernoff’s Inequality

  $$P(X\geq a) \leq \frac{E(e^{tX})}{e^{ta}}$$

Concentration Inequalities

Hoeffding Lemma Let r.v. $X$ satisfy $E(X) = 0$ and $X\leq b$, Then for any $h>0$

$$E(e^{hX}) \leq e^{\frac{1}{8}h^2 (b-a)^2}$$

Hoeffding Inequality Let the r.v. $X_1,X_2,…,X_n$ be independent, with $x_k\leq X_k\leq b_k$ for each $k$, Let $S_n = \sum_{k=1}^n X_k$. Then

$$P(|S_n- \mu|\geq t) \leq 2e^{-\frac{2t^2}{\sum_{k=1}^n(b_k-a_k)^2}}$$

.